|
Bob - Penrose Tiling Generator and Explorer

Bob is a Microsoft Windows program designed to produce and explore
rhombic Penrose tiling comprising two types of rhombus which together form an
infinite, aperiodic plane. In particular, Bob allows the user to
discover and examine geodesic "walks" within the tiling, some of which display
beautiful, complex, five-fold symmetrical patterns - "Flowers". These
Flowers appear to increase indefinitely in size and complexity as the tiling
grows in extent.
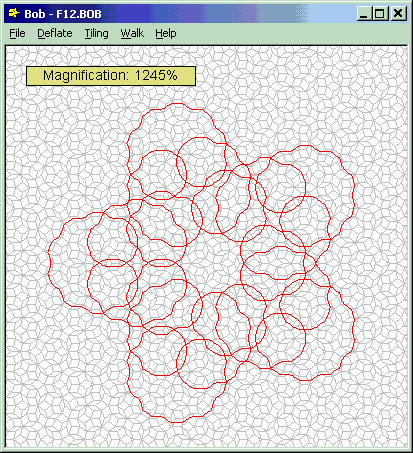
|
Bob - a Windows-based Penrose Tiling generator and explorer.
Click here to download and run the software. When
prompted, chose to Open or Run the
installation prgram - BobI.exe.
March 2022 Update
The 'Bob' application was written (some decades ago)
in C++ using the Microsoft Foundation Classes (MFC). You can download the source code
in a ZIP file by clicking here. You will probably get a
warning about the dangers of downloading ZIP files from unknown sources but
I promise that there are no nasties in the file.
The solution builds successfully using MS Visual Studio 2019 (assuming you have
installed the MFC libraries), albeit with quite a few warnings from differences
between the MS development environment today and that from when the software was
written. The best way to see the code in action is to first install the app using
the link above and then download and run the solution from within VS. This ensures
that the necessary folders and config files are created.
|
Bob is so named after my father, Dr. Bob Collins, who discovered these
walks within rhombic Penrose tiling while working as a member of the Physics
Department of the University of York in England. For a more technical
description of the work, done with Tohru Ogawa of the University of Tsukuba,
Japan, see the
published article. For the mathematically-minded, a technical
document in Adobe PDF format describing various aspects of Penrose tiling can
be downloaded by clicking here.
(It comprises scanned pages which in turn were produced by photocopying a book
20 or so years ago, so please forgive its slightly messy nature). The PDF file
is also rather large (c. 9MB), so please be patient if it does not appear
instantaneously!
 Dr. Bob Collins Dr. Bob Collins
Feel free to email
me with any problems or comments with the software.
Back to Top
There is a wealth of information online about Penrose Tiling, which was
discovered by the British mathematician and physicist Roger Penrose, which I do
not propose to duplicate here. Briefly, Bob deals with the type of
Penrose tiling comprising two types of rhombus of equal side length.
Skinny Rhombi have interior angles of 36º and 144º; Fat Rhombi have interior
angles of 72º and 108º. These two types of rhombi can be fitted together
to form an infinite, aperiodic (i.e. non-repeating) tiling. All
references to Penrose Tiling within this Web site pertain to this type of
tiling.
For more information, see Penrose's book The Emperor's New Mind: Concerning
Computers, Minds, and the Laws of Physics , Oxford University Press,
1989.
Back to Top
Deflation is the process of producing planes of Penrose Tiling by splitting each
individual rhombi of an existing plane into adjacent clusters of smaller
rhombi. All these new clusters collectively make up the next "generation"
of the tiling. The ratio of the side length of new rhombi to that of
their "parent" rhombus is equal to the Golden Mean (1.618033...).
The splitting up of individual rhombi is done according to strict geometrical
rules to ensure that the tiling increases indefinitely in size (as measured by
the number of rhombi contained) without aberrations occurring. In
particular, each rhombus has a specific orientation, which is of no subsequent
relevance to the discovery and investigation of the geodesic walks, and so is
not displayed by Bob.
Bob starts off with a single rhombus - fat or skinny - as the initial
seed for a tiling, and uses deflation to produce successive generations of
tiling. The number of rhombi in any given tiling is larger than its
predecessor by a factor converging on (approximately) 2.6 as the number of
deflations increases.
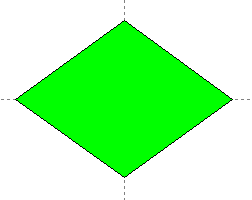
| Each Fat Rhombus deflates into five smaller rhombi - three fat and
two skinny. |
 |
becomes |
 |
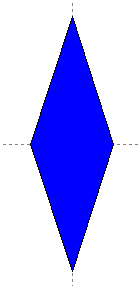
| Each Skinny Rhombus deflates into four smaller rhombi - two skinny
and two fat. |
 |
becomes |
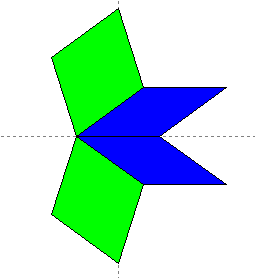 |
Thus the side length of the rhombi in successive generations from a single seed
is inversely proportional to the number of deflations required to produce the
tiling.
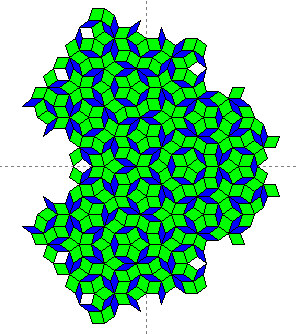
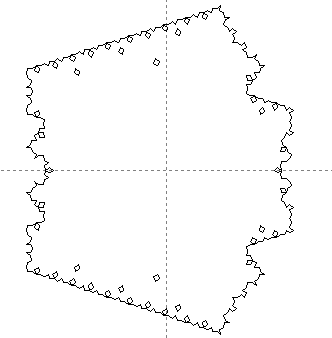
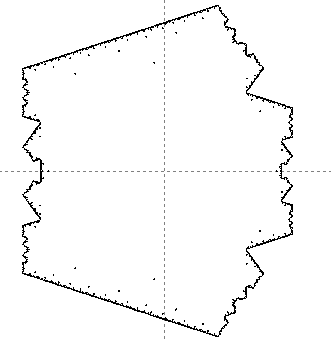
As the number of deflations increases, the shape and area of the tiling
converges. Below are the perimeters of the eighth and twelfth generations
produced from an initial Fat Rhombus, shown at the same scale.
| Eighth Generation - 3,603 rhombi |
Twelfth Generation - 179,234 rhombi |
 |
 |
Again, more details about the process of deflation, including the specific
geometric rules for splitting up existing rhombi into smaller ones, can be
found elsewhere on the Internet.
Back to Top
Redundancy is inherent in the deflation process. When adjacent rhombi are
deflated, they will often produce a pair of child rhombi which are identical in
type, position and orientation, one exactly "covering" the other. These
redundant pairs are trapped during the deflation process by Bob, and one
rhombus of each redundant pair (chosen arbitrarily) is eliminated in order to
guarantee a correct deflation, and thus a tiling without aberrations.
Another characteristic of deflation is that as the tiling grows, it often
surrounds "holes", typically near the perimeter of the tiling, which can then
persist from one deflation to the next. These holes do not signify an
error in the deflation process.
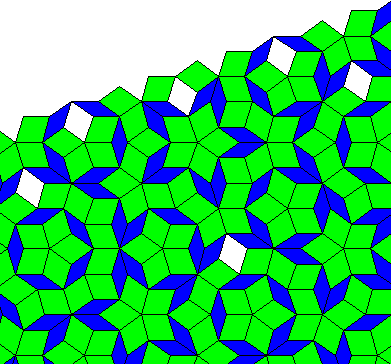
Back to Top
Now comes the interesting bit.
Dr. Collins discovered that, by following certain simple rules for traversing
rhombic Penrose Tiling, a variety of different patterns or "walks" becomes
apparent within the structure of the tiling. The first step in tracing
these walks is to mentally convert the rhombic tiling into a triangular
tessellation by inserting an extra edge across the shorter diagonal of each
rhombus. Then chose an arbitrary vertex within the tiling as a starting
point, and chose an arbitrary edge extending out from the vertex. Follow
this edge until you reach the next vertex, and then take the first edge on
your left (or right). Follow this edge until the next vertex and then
take the first edge on your right (or left). Carry on alternating between
left and right to trace out the walk thus:
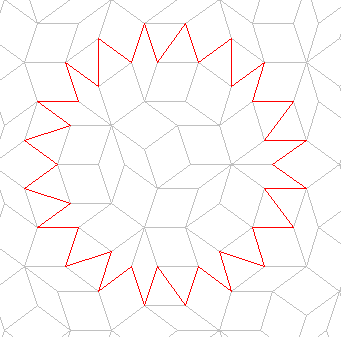
"Spiky" walks such as the closed loop displayed here can be difficult to follow
visually, so for the sake of clarity, by default Bob displays walks by
joining the midpoints of adjacent steps of the walk, thus:
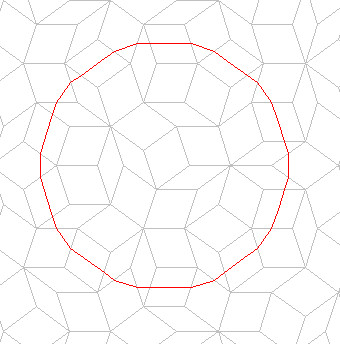
All subsequent images of geodesic walks in this Web site use this simplified,
non-spiky display mode.
Back to Top
Above is an example of a walk (a Small Circle) whose path is roughly
circular, and comprised of 40 steps. A larger version (a Large Circle)
contains 80 steps, an example of which is displayed below:
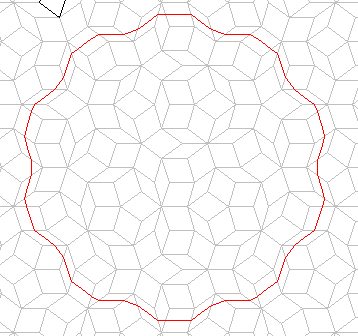
The perimeter of the Large Circle is more wobbly than that of the Small Circle,
but it is classified as a circle nevertheless. As yet, no circles of more
than 80 steps have been discovered.
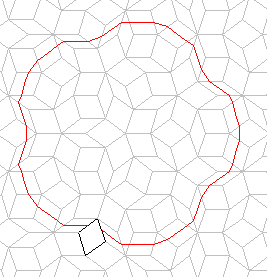
The walk displayed below may also seem to warrant classification as a circle for
the same reason as a Large Circle, but in fact its five-fold symmetry means
that it is classified as a Flower (see later).
The walk displayed below is something of an oddity, in that its symmetry is
unlike that of any other walk discovered within the tiling. It has been
christened a Peanut, and has 48 steps. The right-hand image shows
the distribution of Peanuts within the ninth generation tiling from an initial
Fat Rhombus.
Some walks (Straight Lines) travel across the tiling without wavering
from a macroscopically straight path. Straight Lines are always oriented
in one of five directions.
The final, and most intriguing classification of walk, contains those which are
self-crossing. These are called Flowers, and are by far the most
complex and beautiful walks found within rhombic Penrose Tiling. The path
of a Flower consists of numerous tight loops back on itself, each loop
overlapping its neighbours by no more than the width of a single rhombus.
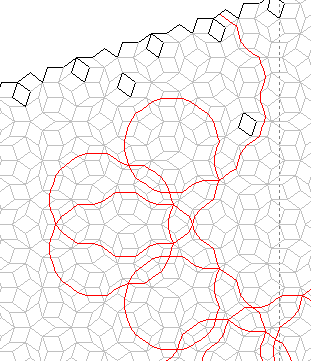
There are two types of Flower - Stars and Pentagons - each
displaying characteristic five-fold symmetry.
| 1,200-step Star |
3,180-step Pentagon |
 |
 |
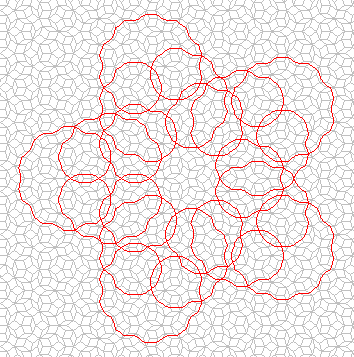
There seems to be no limit to the size and complexity of Flowers. The more
rhombi there are in the tiling, the larger the Flowers contained within
it. Equally, no matter how large the tiling, there are always Flowers
which extend tantalizingly beyond the perimeter. The left-hand image
below displays part of what appears to be a very large Star (although the
self-similarity of the Flowers at different scales makes it difficult to know
for sure). This incomplete fragment of walk alone contains over 33,000
steps. The right-hand image is a detail of bottom of the same walk, to
illustrate the scale.
The self-similarity at different scales mentioned above is illustrated more
clearly below. The left-hand image shows a magnified view of the centre
of the walk shown above - the shape of this small section of the walk mimics
the overall shape of the walk shown above. Similarly, taken in isolation,
the three right-hand points of the partial walk in the left-hand image below
are indistinguishable from the corresponding points of the 4,740-step Star in
the image to its right.
Back to Top
The simplest way to create a new geodesic walk within a given tiling is to first
specify the starting point of the walk by double-clicking the right-hand mouse
button on the targeted rhombus. This brings up a window allowing the user
to specify the direction that that the walk should take:
The legend in bold at the top of the popup window ("Click on first vertex")
prompts the user to select the starting vertex of the new walk by clicking on
its numbered circle covering the desired vertex. Having selected the
starting vertex, the next is selected in the same way. Finally, the user
chooses to turn either left or right at this second vertex, and the walk is
then determined.
Note that, by default, the rhombus selected as the starting point of the walk is
highlighted in red on the tiling underneath the popup window. The Switch
button allows the user to change the starting rhombus to any of its neighbours
on the tiling. Pressing and holding down Alt-S on the keyboard
makes the selected rhombus dance around in a pleasing fashion.
Once the walk has been determined by selecting first and second vertices and a
turn direction, clicking on OK
will remove the popup window and the walk will be displayed.
Walks can also be discovered automatically by Bob using the AutoWalk
feature on the Walk menu.
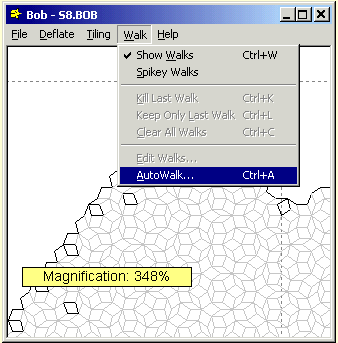 |
Selecting this option displays the AutoWalk window, which is
rather confusing and badly designed. When I get a chance I'll rebuild it
in a more intuitive and sensible way. In the meantime, it can be used to
automatically find walks of various types and lengths within the current
tiling. |
Back to Top
So, what does it all mean? What is the significance of the symmetry and
complexity of the Flowers? Do they extend infinitely, getting more and
more complex, with more and more levels of fractal-like self-similarity?
I have no idea. Feel free to use the software and
see if you can work it out for yourself, and
email me with any questions or comments. Bob can be
downloaded and installed from the "use the software" link above - when
prompted, chose to Open or Run the
installation program, BobI.exe.
Back to Top
PhiMatrix
Written by Gary Meisner: "PhiMatrix is a design and analysis application for Windows or Mac inspired by Phi, the Golden Ratio. Use it to
unveil the beauty of nature's proportions or apply it to your own designs and artistic creations. It overlays
a variety of tranparent grids over any other program to let you see and apply the golden ratio and other proportions
to any image, and is a great tool to achieve excellence in design and composition."
Penrose Patio
Michael Fricke: "Inspired by Dan Schectman's discovery of quasicrystals, an Ohio chemist made this Penrose patio in his backyard."
Back to Top
|